怎麼用微分分析儀（來殺人）

微分分析儀是一種能夠求解微分方程的機械式模擬計算機。它已經不再使用了，因為如今最便宜的筆記本電腦都能更快地解決相同的問題，並且你還可以同時在線刷劇。然而在數字計算機發明之前，微分分析儀使數學家能夠完成一些用其它工具不可能完成的計算。

現如今很難想像一台不是由印刷的數字電路組成的計算機竟然是可以正常運作的。機械計算機聽起來就像是從蒸汽朋克小說里跑出來的一樣。事實證明微分分析儀不但能用，而且還是一些研究領域中必不可少的工具。它最為人所知的應用是曾被美國陸軍用於編製火炮射表。如果沒有射表輔助瞄準，口徑再大的火炮也無法充分發揮效能。所以理論上來說，微分分析儀在幫助同盟國贏得二戰上發揮了重要作用。

要弄清微分分析儀是如何做到這些的，你首先得知道什麼是微分方程。已經還給學校了？沒事，我也一樣。

微分方程

你首次接觸微分方程應該是在大學《微積分 I》的最後幾周。在學期的這個階段，你那薪資低微的兼職教授應該已經教授過極限、導數和積分這些概念了。在這些概念之上再引入等號，現在你就得到了一個微分方程。

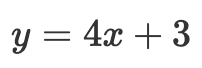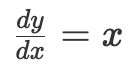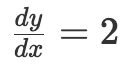微分方程描述了一個變數相對於另一個（或多個）變數的變化率。形如 的常見代數式表示變數 y 與 變數 x 之間的關係。形如 或 的微分方程表示變化率與其它變數間的關係。本質上微分方程就是用純數學方式來描述變化率。前面第一個方程表示 「變數 y 相對於變數 x 的變化率剛好等於 x 。」第二個方程表示「無論 x 的值是多少， y 相對於 x 的變化率總是 2。」

微分方程非常有用，因為在現實世界中，描述複雜系統從一個瞬間到下一個瞬間的變化往往比想出一個描述系統在所有可能的瞬間的方程要容易。因此，微分方程被廣泛應用於物理和工程領域。一個著名的微分方程是 熱傳導方程 heat equation 。它能描述熱量在物體中的擴散過程。要提出一個完全地描述物體在某時刻 t 的熱量分布的函數很困難，但推理熱量從某時刻到下一個時刻的擴散過程不太可能會讓你絞盡腦汁——近冷者變熱，近熱者變冷。所以儘管熱傳導方程在形式上比起前面的例子要複雜得多，它也只是變化率的描述而已。它描述了在給定與周圍的溫差時，物體上任意一點的溫度隨時間的變化。

再來舉一個更具體的例子。假如我在真空中豎直向上拋出一個網球，在我窒息之前它會落回來嗎？這是我在高中物理課上被問到的問題，解決它只需要基本的牛頓運動方程。現在暫且假設我已經忘記了牛頓運動方程，只記得物體以恆定的加速度 g （大約為 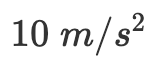）向地球加速運動。那麼如何用微分方程來解決這個問題呢？

現在把我對高中物理僅存的記憶表示成微分方程。網球在離手後會向地球以 g 加速運動。也就是說網球的速度相對於時間的變化率為 g（在負方向上）。進一步，我們可以說球離地高度的變化率（也就是速度）隨時間的變化率是負方向的 g 。其微分方程形式如下，其中 h 表示高度， t 表示時間：

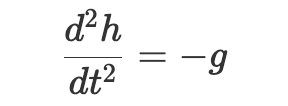
它跟前面的微分方程看起來略有差別，因為這是所謂的二階微分方程。我們討論的是變化率的變化率，也許你還記得微積分課講過，這需要用到二階導數。這是方程左邊部分看上去像被平方了的原因。但是該方程也僅僅表示了球向下以恆定的加速度 g 加速運動這一事實。

到這裡，我可以選擇使用微積分來求解微分方程。解微分方程並不是要找滿足指定關係的值，而是要找滿足關係的函數。對上面的微分方程的另一種理解是存在這樣的函數，它的二階導數為 -g 。我們想要找到這個函數，因為它能告訴我們球在任意時刻的高度。好在這個微分方程恰巧是容易求解的。通過這樣，我們可以重新推導出那些被我遺忘了的運動方程，從而輕鬆地計算出球落回來所花的時間。

但是大部分情況下微分方程是很難求解的。有時甚至是無法求解的。假設我在大學時把更多的精力花在了計算機科學上，那麼我的另一種選擇就是用微分方程來做模擬。如果已知球的初速度和加速度，我可以輕易用 Python 寫一個 for 循環來逐秒迭代計算球在離手後 t 時刻的速度。在此基礎上對循環程序稍加修改，就可以用算出的速度迭代計算出球的高度。運行這個 Python 模擬程序，它就可以計算出球什麼時候落回來了。這個模擬並不是完全精確的，但是我可以通過減小計算用的時間步長來提升精度。總之我要做的只是搞清楚當球落回來時我是否還活著。

這就是微分方程的數值解法。這也是大多數領域中求解微分方程時實際採用的方法。對於用數值方法求解微分方程，計算機是必不可少的，因為模擬的精度取決於在微小步長上進行的大量計算。手工計算容易出錯並且太耗時。

那如果將這個問題的背景時間設定在 1936 年呢？我仍然希望實現計算過程的自動化。但是此時離 克勞德·香農 Claude Shannon 完成他的碩士論文還有一年時間。在這篇論文中香農用數字電路實現了 布爾代數 boolean algebra 。沒有數字計算機可用，恐怕就只能寄希望于于模擬計算機了。

微分分析儀

首台微分分析儀是由 范內瓦·布希 Vannevar Bush 和 哈羅德·哈森 Harold Hazen 於 1928 年到 1931 年在 MIT 建造的。他們兩人都是工程師。製造它是為了解決應用數學和物理領域中的實際問題。正如布希在 1931 年的一篇論文 中所說，微分分析儀是為了解決那些「不斷為他們所用方程的複雜性而不是深刻性所困擾的」的數學家的所面臨的當代問題。

微分分析儀是一台由傳動軸、齒輪和轉盤組成的複雜儀器，它能夠求解高達六階的微分方程。它是一台由簡單部件通過複雜組合而成的神奇機器。在這一點上它和數字計算機很像。不同點是，數字計算機通過在電路中實現布爾代數來模擬代數問題，而微分分析儀通過傳動軸、齒輪和轉盤直接模擬微分方程問題。微分分析儀的本質就是對實際問題的直接機械類比。

那到底怎麼用齒輪和轉盤來計算微積分呢？其實這是最容易解釋的部分。微分分析儀最重要的構件是六個積分器，每一個對應一階的微分方程。機械積分器的歷史可以追溯到 19 世紀，它是一個相對簡單的裝置，能夠對單個簡單函數進行積分運算的。下面我們將了解積分器的工作原理，但順便說一句，布希的巨大成就不是發明了機械積分器，而是發現了一種將積分器串聯起來解決高階微分方程的方法。

機械積分器由一個大轉盤和一個小得多的轉輪組成。轉盤像唱片機的轉檯一樣平行於地面平放。它由電機驅動勻速轉動。轉輪豎直的輕放於轉盤表面上，其壓力既要足夠讓轉盤驅動轉輪，又不能太大以致於阻礙轉輪相對於轉盤自由側向滑動。總之當轉盤轉動時，轉輪也跟著轉動。

轉輪的轉速由它距離轉盤中心的距離決定。轉盤的中心部分自然轉動得比邊緣部分慢。轉輪的位置是固定不動的，而轉盤被安裝在一個可以來回滑動的底座上。這樣就可以調節轉輪相對轉盤中心的位置。下面就是積分器工作的關鍵原理：轉盤底座的位置由積分器的輸入函數控制。積分器輸出取決於轉輪的轉動量。所以輸入函數驅動了輸出函數的變化率，這就是將某個函數的導數轉換成了這個函數本身。這不就是積分運算嗎？

如果剛才的解釋還沒有讓你理解積分器的原理，那麼直接看到機械積分器實際工作的樣子應該對你有所幫助。其實它的原理出乎意料的簡單，看一遍它的運行過程你肯定就能窺見其運作機制。因此我製作了一個 運行中的機械積分器動態原理圖，強烈建議你看一看。它展示了通過各個部件的旋轉和移動求函數 f(x) 的 不定積分 antiderivative F(x) 的過程。這可太有趣了。

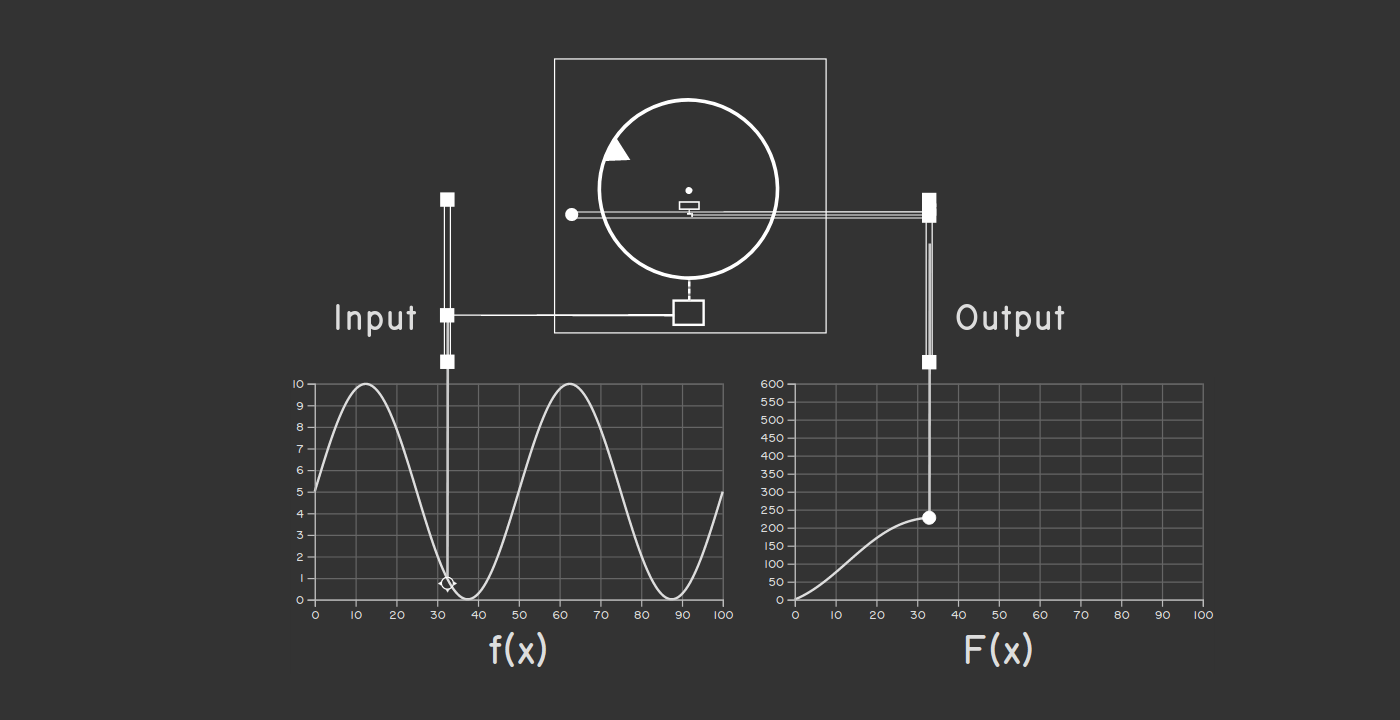
現在我們有了可以做積分運算的組件，但是只靠它還不足以解決微分方程。為了解釋求解微分方程的全過程，我將使用布希在他 1931 年的論文中所舉的例子。這個例子恰巧跟前面考慮的微分方程是在本質上是一樣的。（真是奇妙的巧合！）布希使用下面的微分方程來表示下落物體的運動：

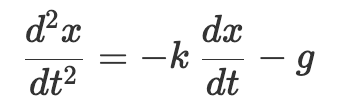
這跟前面的網球運動的方程基本上是一樣的，只不過布希使用 x 代替了 h ，並且增加了一項來表示空氣阻力的減速作用。這個新增項採用了最簡單的形式來描述空氣阻力的作用：空氣減慢球速的比率正比於球的速度（這裡 k 是一個常比例係數，我並不關心它的具體取值）。也就說是球運動得越快，空氣阻力就越大，對球的減速作用越顯著。

為了配置微分分析儀來解決這個微分方程，我們需要從布希稱之為「輸入面板」的東西開始。輸入面板其實就是一張安裝在支架上的坐標紙。如果想要解更複雜的方程，首先需要操作員在坐標紙上繪製好輸入函數圖像，然後在機器啟動時用一個與機器主體相連的指針來跟蹤函數圖像的軌跡。在我們舉的例子中，輸入是常數 g ，所以我們只需將指針移動到正確的位置並讓它保持不動即可。

剩下的變數 x 和 t 又是什麼呢？變數 x 表示球的高度，是微分分析儀的輸出。它會被繪製在輸出面板上的坐標紙上。輸出面板與輸入面板類似，只是它沒有指針，取而代之的是由微分分析儀驅動的繪圖筆。變數 t 僅僅是按固定速率步進。（在前面模擬網球運動 Python 程序中，我們通過循環來增加 t 。）變數 t 來源於微分分析儀的電機，它通過勻速轉動傳動軸來驅動整個計算過程。

布希的原理圖對於理解我下面要介紹的內容很有幫助。不過為了便於理解，需要先對微分方程再做一次變換。對方程兩邊同時進行一次積分，得到下式：

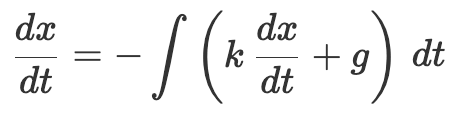
現在方程中的各項與微分分析儀運行中各部件轉動量所表示的值之間有了更明確的對應關係。布希的原理圖如下：

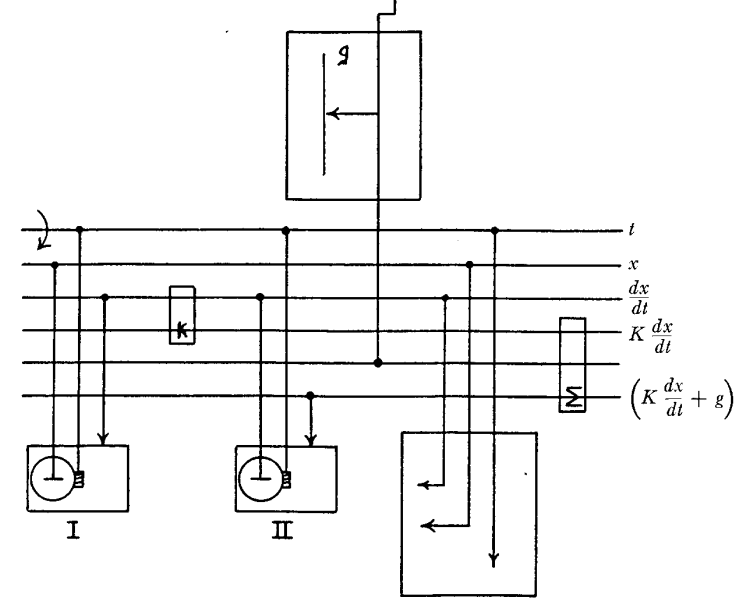
在原理圖的頂部是輸入面板，右下角是輸出面板。

圖中的輸出面板被配置成同時繪製高度 x 和速度 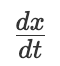。積分器在左下方，由於這是二階微分方程，所以我們需要兩個積分器。電機驅動頂部標註為 t 的傳動軸。（有趣的是，布希將這些水平傳動軸稱為「匯流排」。）

現在原理圖中還剩下兩個部件沒有解釋了。裡邊標記了 k 的方框是 乘法器 multiplier ， k 是比例常數。它獲取由 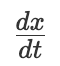標記的傳動軸的轉動量，並通過齒輪組進行放縮。用 ∑ 標記的方框是 加法器 adder 。它通過巧妙的齒輪組合將兩個傳動軸的的轉動疊加起來驅動第三個傳動軸。我們的方程中涉及了求兩項之和，所以需要引入加法器。這些額外組件的引入確保了微分分析儀有足夠的靈活性來模擬由各種各樣的項和係數組成的方程。

我發現以慢放的方式來推演電機啟動時的級聯因果過程對於理解微分分析儀的原理很有幫助。電機啟動後立即驅動傳動軸 t 勻速旋轉。這樣我們就有了時間的概念。這個傳動軸有三個作用，分別由連接其上的三個豎直傳動軸表示：它驅動了兩個積分器的轉盤的轉動，同時帶動輸出面板的支架讓繪圖筆作圖。

如果積分器的轉輪被放置在轉盤中心，那麼傳動軸 t 就不會帶動其它傳動軸轉動。積分器的轉盤會轉動，但是放置在轉盤中心的轉輪不會被帶動。這時輸出圖像將會是一條平坦的直線。出現這種情況是因為我們沒有明確指定問題的初始條件。在上面的 Python 程序中，我們需要以常量或函數參數的形式用到網球的初始速度。在啟動機器之前，我們通過將兩個積分器的轉盤調整到合適的位置來指定速度和加速度的初始值。

設置好這些之後，傳動軸 t 的轉動將會傳導到整個系統之中。從物理上來說，許多部件會同時開始轉動。但是我們可以認為轉動首先傳導到積分器 II，然後與基於 g 計算得到的加速度表達式求積分得到球的速度 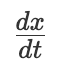。速度又反過來作為積分器 I 的輸入，推動它的轉盤讓輸出轉輪以速率 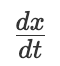轉動。積分器 I 的輸出作為最終結果將會被直接導向到輸出面板上。

前面我有意避開了一個令人困惑的細節，那就是機器里有一個怪圈。積分器 II 以傳動軸 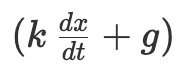為輸入，但是該傳動軸的轉動又部分決定於積分器 II 的輸出本身。這可能快把你繞吐了，但在物理上這並沒有任何問題——因為所有部部件都是一同轉動的。出現這種怪圈並沒什麼奇怪的，因為在用微分方程在描述某函數的變化率時，也經常會用該函數的函數的形式。（在這個例子中，加速度，即速度的變化率，取決于于速度。）

在將所有東西都正確配置好後，機器會輸出球的高度和速度隨時間變化的函數圖像。這個圖像是紙質的。用我們的現代數字化思維來看，這可能有點難以理解。畫在紙上的函數圖像能幹什麼？微分分析儀確實不能魔術般地給出解的簡潔數學表達式，這是事實。但也請記住一點，很多的微分方程根本沒有簡潔的解析解。紙上的函數圖像與前面模擬球下落的 Python 程序包含相同的信息：某時刻球的位置。它可以回答任何關於該問題的實際問題。

微分分析儀簡直酷到爆。它雖然結構複雜，但是本質上只是一些傳動軸和齒輪外的組合。要理解它的運作過程，你不必是電氣工程師或者會製造晶元。然而它確實可以解微積分！它能夠求解出那些靠你自己永遠無法解決的微分方程問題。它證明建造計算機器的關鍵材料不是硅而是人類的創造力。

殺人

人類的創造力既能為善，也能為惡。正如我提到的，微分分析儀在歷史上最知名的應用是為美國陸軍計算火炮射表。鑒於二戰是一場「正義的戰爭」，這是最好的結果。但是也不能忽視微分分析儀增強了大口徑火炮的殺傷效能。火炮的確殺死了很多人。如果維基百科可信的話，在二戰中死於炮火的士兵比被輕武器殺死的更多。

我們稍後再回到道德討論上來，先快速解釋一下為什麼計算射表這麼困難，以及微分分析儀是怎麼幫助計算射表的。這是將微分分析儀應用於實際問題的很好的例子。射表能告訴炮手在射擊某個距離外的目標時需要將炮口上抬多高。編製射表的一種方法是在不同的仰角下發射該火炮，並將結果記錄下來。這種方法被用在靶場，比如位於馬里蘭的阿伯丁試驗場。但是單純通過實驗觀察的方式來編製射表即昂貴又耗時。在考慮到如天氣狀況或不同彈丸重量等其它因素時，需要進行的射擊次數將會隨組合爆增到無法實施的程度。所以基於少量觀測數據建立數學模型，再基於該模型來填充出完整的射表是一個更好的方法。

我不想太深入討論這些數學理論，它們實在太難了，我也不懂。但是你應該也想到了，支配飛行中的炮彈和向上拋出的網球運動的物理規律並沒有什麼不同。由於計算精度的需要，我們使用的微分方程不得不偏離其理想化的形式，並迅速變得面目猙獰起來。即便是最早的精確彈道理論中的公式，除其它因素外，還考慮了彈丸的重量、直徑、形狀、主風、海拔、大氣密度以及地球自轉 ^[1] 。

雖然關於射表計算的方程很複雜，但它們跟前面的微分方程一樣，都可以通過微分分析儀數值求解。1935 年微分分析儀被阿伯丁試驗場用於求解彈道方程。這顯著加快了計算射表的速度。 ^[2] 然而，二戰期間對於射表的需求增長太快了，以至於美國陸軍計算射表的速度難以滿足運往歐洲戰場的武器裝備的配套需求。這最終導致陸軍資助了賓夕法尼亞大學的 ENIAC 項目。這促成了世界上第一台數字計算機的誕生。（LCTT 譯註：嚴格來說 ENIAC 是第二台電子數字計算機。第一台電子計算機是 阿塔納索夫-貝瑞計算機 Atanasoff–Berry Computer ，簡稱 ABC 計算機。）ENIAC 能夠通過重新布線運行任意程序。但建造它的主要是為了以數倍於微分分析儀的速度來計算射表。

鑒於在微分分析儀之外，射表計算問題極大地推動了早期計算領域的發展，專門挑出微分分析儀的道德問題也許是不公正的。微分分析儀並沒有局限于軍事領域的應用，在二戰期間和二戰後的很大一段時間裡，由於美國軍方投入的大量的撥款，整個計算領域得到了發展。

總之，我認為微分分析儀更有趣的遺產是它告訴了我們計算的本質。我驚嘆于于微分分析儀能做到這麼多事情，我猜你也一樣。我們很容易落入這樣的思維陷阱：將計算看作是由快速數字電路實現的領域。事實上，計算是更抽象的過程，電子數字電路只是實現計算的典型手段罷了。在關於微分分析儀的論文中，布希說他的發明不過是在「運用複雜機械結構來類比複雜的推理過程這一影響深遠的計劃」上的微小貢獻。他的總結很貼切。

1. Alan Gluchoff. 「Artillerymen and Mathematicians: Forest Ray Moulton and Changes in American Exterior Ballistics, 1885-1934.」 Historia Mathematica, vol. 38, no. 4, 2011, pp. 506–547., https://www.sciencedirect.com/science/article/pii/S0315086011000279. ↩︎
2. Karl Kempf. 「Electronic Computers within the Ordnance Corps,」 1961, accessed April 6, 2020, https://ftp.arl.army.mil/~mike/comphist/61ordnance/index.html. ↩︎

via: https://twobithistory.org/2020/04/06/differential-analyzer.html

作者：Two-Bit History 選題：lujun9972 譯者：toknow-gh 校對：wxy

本文由 LCTT 原創編譯，Linux中國 榮譽推出

本文轉載來自 Linux 中國: https://github.com/Linux-CN/archive